Probabilities and Tail Events in the Game of Investing
- Vishal Barfiwala
- Sep 2, 2021
- 6 min read
Updated: Sep 7, 2021

What is the probability of picking a card from a standard deck of 52 cards, which is red and is numbered? - Math paper, most schools
Since secondary school, we are taught to calculate probabilities with a coin, dice, a pack of cards, an urn with a counted number of red and white balls. And we learn this usually by listing out all possible outcomes and assigning probabilities based on the number of times an event can occur. You will notice that most of these are used in 'games', often in a casino. One of the few places in life where the odds are predetermined (and always in favor of the house).
We then graduate to probability distributions - Binomial, Poisson, and the Normal 'Bell' curve among others. In such cases a curve, which is drawn based on values assigned to Greek alphabets such as μ, σ, 𝛘, etc. We try to 'simulate' real world events with problem statements such as - “If 300 vehicles pass through a busy junction in an hour, what is the probability that none pass in a given minute?” And we 'confidently' give a 'certain' probability number.
Not making a special mention about the Gaussian Normal distribution or the Bell curve is as commonly called, would do injustice to this topic. Apparently most of the important things in life follow this curve, be it - grades in college, heights of school kids in a classroom, IQ levels in a population, balls dropped in a Galton board, and, of course, stock price returns. Let's get some data into the picture, by looking at the 1-day returns of S&P BSE Sensex index from Jan 1986 (since inception) until May 2021 (when I took the data) which has over 8,000 data points. Now let's plot the 1-day returns across ranges on a chart, which shows the number of times the index has given a return in a specified range - essentially a Histogram (e.g., 878 times the Sensex has a 1-day return between 0% and 0.3%).
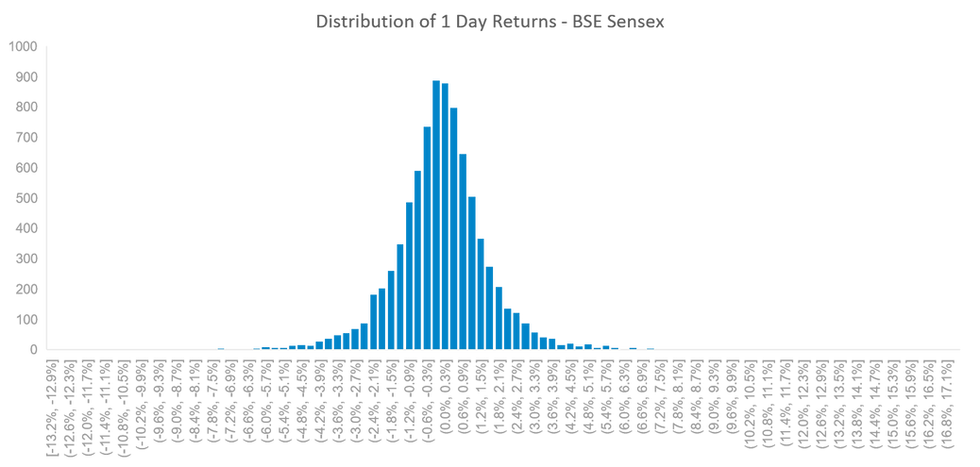
As you would have guessed, this looks like our favorite Bell curve. Let us go ahead and approximate this to the Normal curve, and try to make decisions based on this. For instance, what is the probability of making a return greater than 10% or less than -10% on a single day? Based on the normal distribution approximation, that would have a probability of 0.0000000012395 or once in 2,210,348 years. Well, in reality, this has occurred 9 times in the last 35 years! Would you bet your wealth on such mathematics? (Unlike the Wall Street quants in 2008, albeit with much more sophisticated models as compared to my trivial approximation to the Normal distribution.)
Nassim Nicholas Taleb, in his bestselling book, The Black Swan, calls this the Ludic Fallacy - the incorrect gamification of real life situations. In reality, we don't (and can't, in most circumstances) know the probabilities of different outcomes. If I were the CEO of a Pharma company, I wouldn't say that there is a 45% chance of earning USD 10 Bn, 25% chance of breaking even, and 30% chance of making a loss of 1 Bn. Actually, I wouldn't even be able to list down the 'possible' scenarios with certainty, let alone assign probabilities to each of them. I am not, for once, suggesting that we should not think in terms of probabilities to assess outcomes. Just that we need to be cognizant that there is always going to be a scenario we have not envisaged, and that the probability of a scenario is more of an estimated range, based on reasonable assumptions in turn based on past experience, rather than a definite number. The guess may be more or less accurate, and the range may be narrow or wide, depending on our level of expertise in that particular situation. If you are a Pediatrician who has examined over a hundred patients everyday over the last 30 years, your diagnosis of a particular ailment, based on a set of symptoms, is going to be pretty accurate in almost all cases. However, there will always be a case where the diagnosis turns out to be incorrect due to a number of reasons, and you will not be able to ‘predict’ when this would occur. The patient ignored mentioning some relevant symptom, or one of the symptoms didn't present itself as it otherwise would, or there was some other coexisting condition which brought its own symptoms to the mix, and the list could go on.
It is, hence, practically impossible to estimate either the timing or the magnitude of ‘tail events’ (which are infrequent in nature). Further, there is a high probability of error in many of our assumptions in determining the probabilities of events, and making decisions based on those. How then can an investor mitigate some of this?
Have a high margin of safety
In the Indian parlance, look for bargains and discounts. This is one of the most well known teachings of Ben Graham (Warren Buffet's guru), and yet, often ignored. How often have we been guilty of buying a stock which has run up substantially, just because everyone around us is talking and raving about its future prospects and we don't want to miss out on the opportunity (experiencing extreme FOMO)? How often do we base the valuation of a company or stock on the hope of an event happening, without considering the implication of that event not happening?
Rather, the more logical approach is to first determine our version of the fair value of a stock or any other investment based on the different scenarios and probabilities we can think of, and then buy it when it is available at a discount, when even if we are wrong in our assumptions, the loss is limited. Of course, this is not easy, bargains are not easily available, and if they are available, they are in out of favor companies which others are running away from. But it never was meant to be easy. It requires strong conviction for us to go against the crowd and be a contrarian to identify and bet on such bargains, and such conviction can only be built through developing an extremely thorough understanding of the market, industry, and the company, which leads us to the next point.
Stay within your Circle of Competence
How many stocks have you invested in over the last year? Which sectors do they belong to? How well do you know these sectors? All of us would be guilty of investing in securities in areas which we don't know or understand too well, yet invest in them due to reasons including ‘others are buying this, and I don't want to miss out on the opportunity’ or ‘I think this EVs are the future and hence, I should get into the race now’ or ‘Rakesh Jhunjhunwala bought this stock’ or a multitude of other reasons.
If we don't understand the industry and business we are investing in, we will never be able to build conviction on the stock we are buying. Without conviction, we will never be able to commit a meaningful capital to the stock, and hence, not be able to get any benefit (or even an impactful loss) from that stock. What we may get is ‘bragging rights’. Also, without that conviction, we would not be able to withstand the volatility in that stock, continuously second-guess the investment and most likely exit when the stock dips, irrespective of its actual prospects, virtually guaranteeing a loss.
What is this circle of competence? - It is the industries, sectors, trades, businesses we understand well. And by understanding them well, we know what drives the profitability of the business, how such a business makes money, what are the dynamics of that industry with competitors, customers, regulation etc., we understand some of the risks being faced by the business. The starting point of this circle is the industry we work in, or the consumer related businesses we have had exposure to as customers, and we should aim to keep expanding this circle though reading and educating ourselves, and learning from people who understand the areas which we wish to expand our circle of competence in. Once we understand the business, we are able to reasonably forecast potential futures of that business and assign more educated probabilities to these futures. But most importantly, we are able to build conviction and stay the course without getting significantly impacted by the daily vagaries of the market.
Diversify, without di-worsifying
The age old adage “Don't put all your eggs in one basket” is as applicable to investing as other areas in life. However, while many of us follow this advice when it comes to stocks, we usually run the risk of ending up with too many baskets. How much of each stock to invest in? Or which asset classes to own and what their allocation should be? These are very individual specific decisions - depending on your age, liabilities, income levels, goals, temperament etc. and there is truly no one size fits all solution in my opinion. However, it is critical to figure this out for yourself, and then size the investments accordingly.
And lastly, keep it simple. There is no point creating complex and detailed spreadsheets which rely upon a number of assumptions building upon each other, when a simple back of the envelope calculation can do the job. As Keynes once said:
“It is better to be roughly right, than to be precisely wrong.”



Comments